好玩的数据结构和算法
快速乘法
计算机喜欢做加法而不喜欢乘法,所以可以想办法把乘法转化为加法来提升计算效率。快速乘法本质上就是利用二进制表示和乘法结合率。例如: \(3 \times 5 \\ = 11_2 \times 101_2\\ = 11_2 \times (100_2 + 10_2 + 1_2)\\ = 11_2 \times 100_2 + 11_2 \times 10_2 + 11_2 \times 1_2 \\ = 11_2 << 2 + 11_2 << 1 + 11_2\)
算法实现:
long long quickMult(long long a, long long b) {
long long res = 0;
while (b > 0) {
if (b & 1) {
res += a;
}
b >>= 1;
a <<= 1;
}
return res;
}
类似的还有快速幂运算。
树状数组(Binary Indexed Tree)
有这样一个需求:
- 保存n个数据,每个数据都可能更新;
- 随时查询这个数组第1~i个元素的和
最简单的方式是直接用一个数组,那么更新的复杂读为$O(1)$,查询的复杂度为$O(n)$。使用树状数组可以将查询的复杂读将为$O(\log{n})$,更新的复杂度也为$O(\log{n})$。
简单来说,树状数组利用数的二进制表示来保证查询复杂读为$O(\log_{2}{n})$,例如$\sum_{1}^{7} = tree[7] + tree[6] + tree[4]$,我画了一个简单示意图,其中方块表示第1~i个元素的和:

网络上的一张示意图:
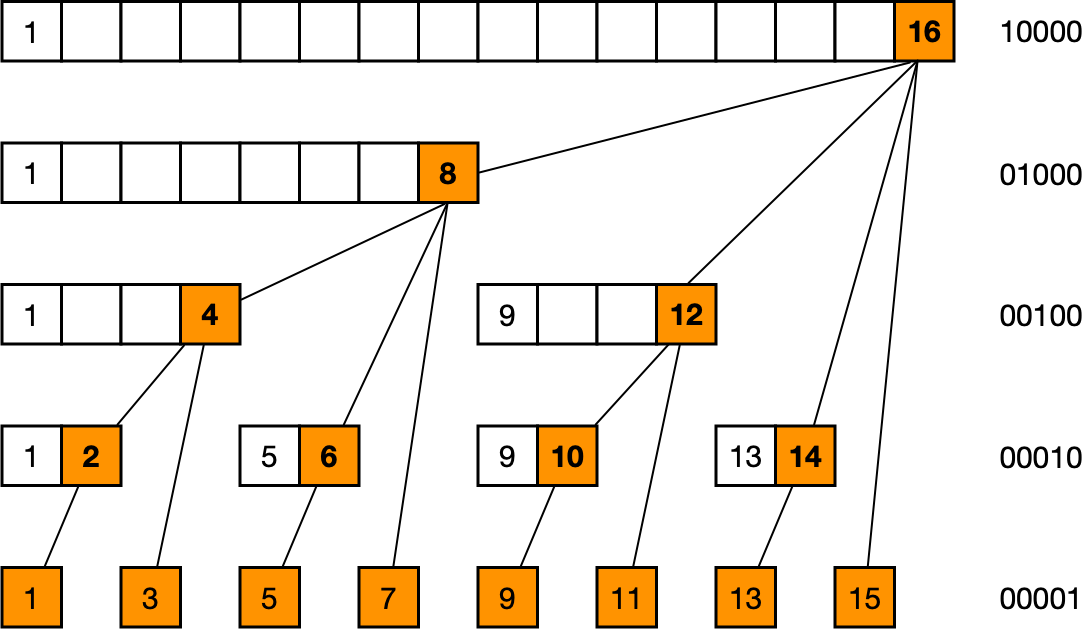
也就是说,tree[i]表示i之前的$2^k$元素之和,其中k是i的二进制表示的右边第一个1之后的零的个数: \(2^k = i \And (\sim i)\)
一个树状数组的实现如下:
class BIT {
vector<int> tree_;
int n_;
public:
BIT(int n) : n_(n), tree_(n_ + 1) {}
void update (int i) {
while (i <= n_) {
tree[i]++;
i += lowbit(i);
}
}
int query(int i) {
int res = 0;
while (i > 0) {
res += tree[i];
i -= lowbit(i);
}
return res;
}
private:
int lowbit(x) {
return x & (-x);
}
}
LeetCode上,树状数组可以用来计算右侧小于当前元素的个数、数组中的逆序对。
线段树
线段树和树状数组有些类似,但实现稍微复杂点,它被用来解决这样的需求:
- 求一个数组中任意一段区间的元素之和,复杂度$O(log(n))$
- 随时可能更新数组中的某个元素,复杂度$O(long(n))$
线段树的思路如图所示:
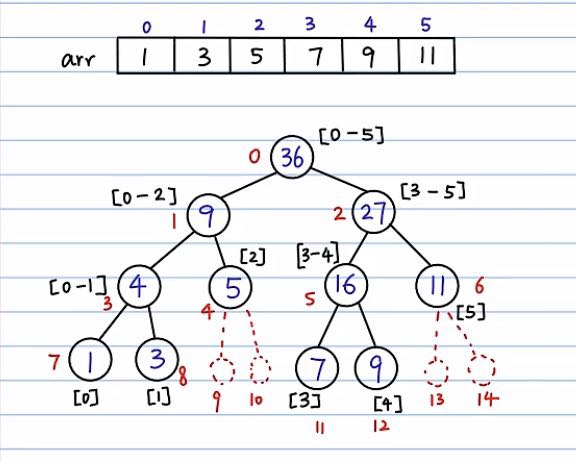
用树的根节点表示n大小数组[0, n - 1]范围的和;然后左子节点表示父节点前半部分[0, (n - 1) / 2]之和,右子节点表示后半部分[(n - 1) / 2 + 1, n -1]之和,以此类推,直到区间内只有一个元素,直接返回该元素结束。
线段树实现的代码如下:
class SegmentTree {
int size_;
vector<int> tree_;
void buildTree(vector<int>& arr, int node, int start, int end) {
if (start == end) {
tree_[node] = arr[start];
} else {
int mid = start + ((end - start) >> 1);
int leftNode = 2 * node + 1;
int rightNode = 2 * node + 2;
buildTree(arr, leftNode, start, mid);
buildTree(arr, rightNode, mid + 1, end);
tree_[node] = tree_[leftNode] + tree_[rightNode];
}
}
int query(int node, int start, int end, int qstart, int qend) {
if (qstart > end || qend < start) {
return 0;
}
if (start >= qstart && end <= qend) {
return tree_[node];
}
int mid = start + ((end - start) >> 1);
int leftNode = 2 * node + 1;
int rightNode = 2 * node + 2;
return query(leftNode, start, mid, qstart, qend) +
query(rightNode, mid + 1, end, qstart, qend);
}
void update(int node, int start, int end, int idx, int val) {
if (start == end) {
tree_[node] = val;
} else {
int mid = start + ((end - start) >> 1);
int leftNode = 2 * node + 1;
int rightNode = 2 * node + 2;
if (idx >= start && idx <= mid) {
update(leftNode, start, mid, idx, val);
} else {
update(rightNode, mid + 1, end, idx, val);
}
tree_[node] = tree_[leftNode] + tree_[rightNode];
}
}
public:
void debugPrint() {
for (auto& node : tree_) {
cout << node << ' ';
}
cout << '\n';
}
SegmentTree(vector<int>& v) : size_(v.size()), tree_(size_ * 4) {
buildTree(v, 0, 0, size_ - 1);
}
void update(int idx, int val) {
update(0, 0, size_ - 1, idx, val);
}
int query(int qstart, int qend) {
return query(0, 0, size_ - 1, qstart, qend);
}
};