CS231n Assignments Note8: Recurrent Neural Network
Table of Contents:
A Try to Interprete The Essence of RNN
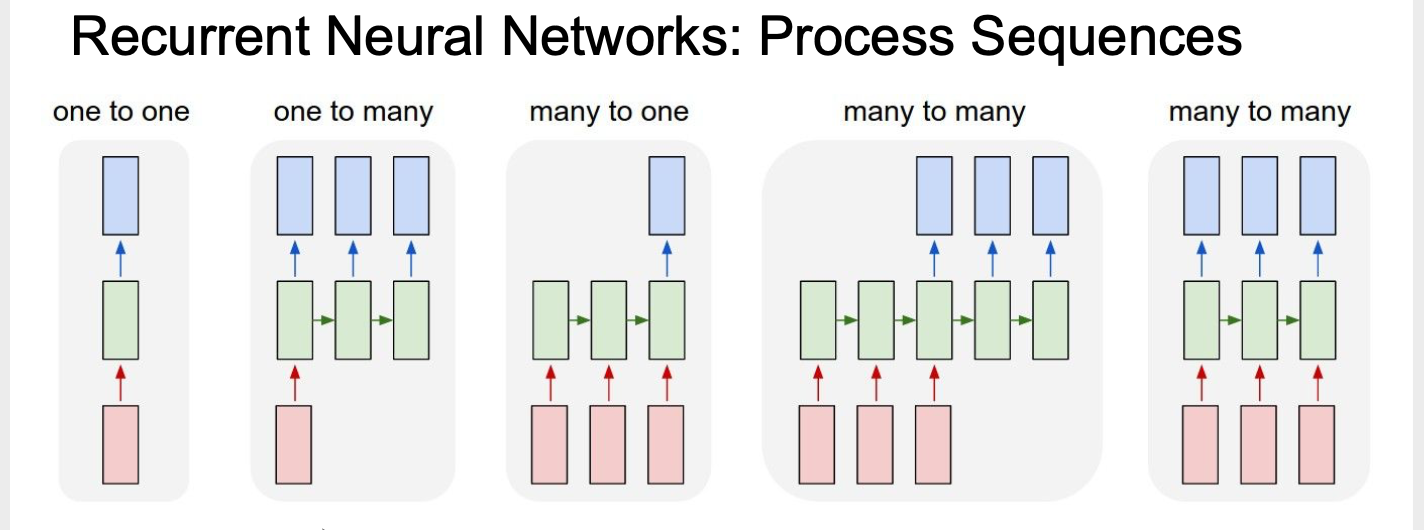
Unlike previous neural network, RNN processing sequence problem, such as image caption for one to many, sentiment classification for many to one, machine translation and video classification for many to many.
A computational gragh looks like this:
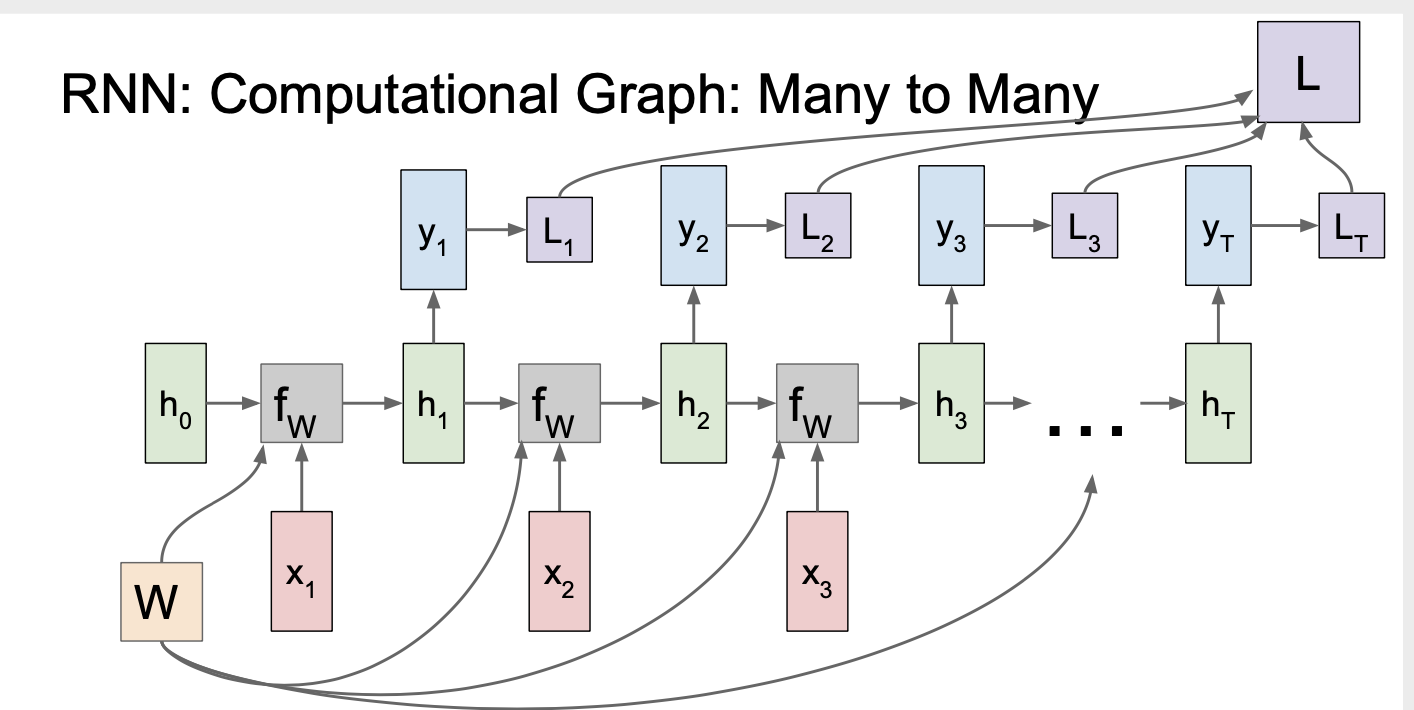
For image caption, we first use pre-trained CNN to output a vector as the input of RNN, look at this picture:
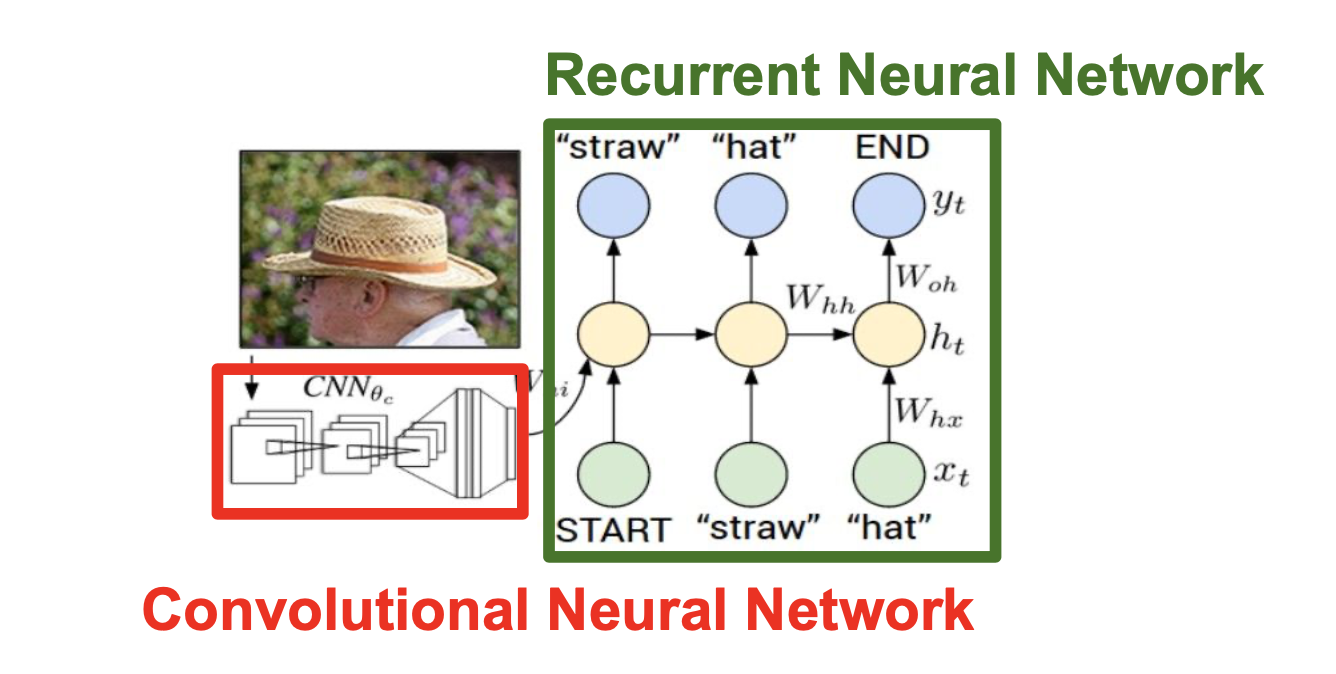
and this sample to help make sense:
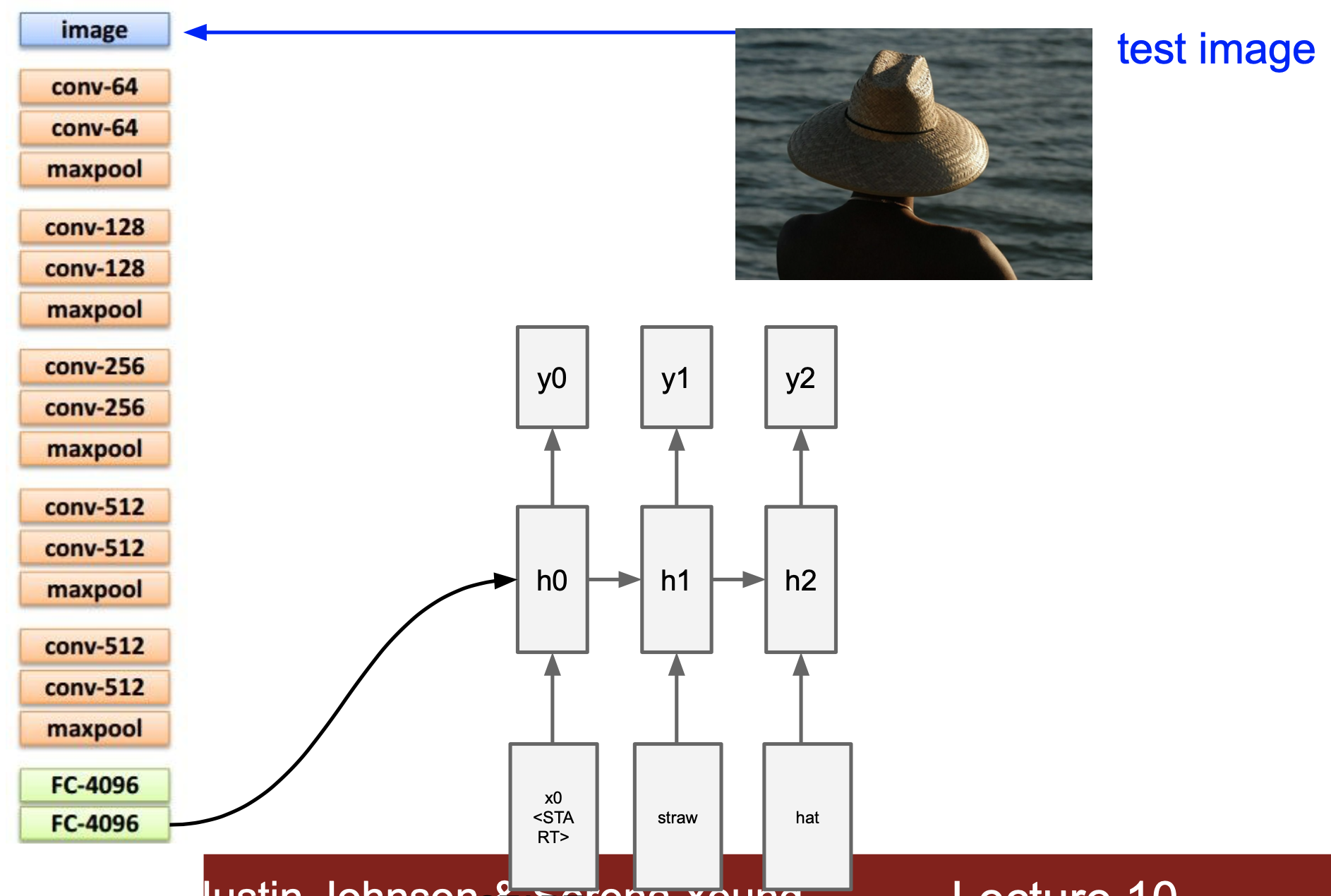
As for the implement, I just paste the key function below:
def rnn_step_forward(x, prev_h, Wx, Wh, b):
"""
Run the forward pass for a single timestep of a vanilla RNN that uses a tanh
activation function.
The input data has dimension D, the hidden state has dimension H, and we use
a minibatch size of N.
Inputs:
- x: Input data for this timestep, of shape (N, D).
- prev_h: Hidden state from previous timestep, of shape (N, H)
- Wx: Weight matrix for input-to-hidden connections, of shape (D, H)
- Wh: Weight matrix for hidden-to-hidden connections, of shape (H, H)
- b: Biases of shape (H,)
Returns a tuple of:
- next_h: Next hidden state, of shape (N, H)
- cache: Tuple of values needed for the backward pass.
"""
next_h, cache = None, None
##############################################################################
# TODO: Implement a single forward step for the vanilla RNN. Store the next #
# hidden state and any values you need for the backward pass in the next_h #
# and cache variables respectively. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x_wx = x.dot(Wx)
prev_wh = prev_h.dot(Wh)
out = x_wx + prev_wh + b
next_h = np.tanh(out)
cache = (x,Wx,Wh,prev_h,out)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return next_h, cache
def rnn_step_backward(dnext_h, cache):
"""
Backward pass for a single timestep of a vanilla RNN.
Inputs:
- dnext_h: Gradient of loss with respect to next hidden state, of shape (N, H)
- cache: Cache object from the forward pass
Returns a tuple of:
- dx: Gradients of input data, of shape (N, D)
- dprev_h: Gradients of previous hidden state, of shape (N, H)
- dWx: Gradients of input-to-hidden weights, of shape (D, H)
- dWh: Gradients of hidden-to-hidden weights, of shape (H, H)
- db: Gradients of bias vector, of shape (H,)
"""
dx, dprev_h, dWx, dWh, db = None, None, None, None, None
##############################################################################
# TODO: Implement the backward pass for a single step of a vanilla RNN. #
# #
# HINT: For the tanh function, you can compute the local derivative in terms #
# of the output value from tanh. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x,Wx,Wh,prev_h,out = cache
dnext_h = dnext_h*(1-np.tanh(out)**2)
db = np.sum(dnext_h,axis = 0)
dWh = (prev_h.T).dot(dnext_h)
dprev_h = dnext_h.dot(Wh.T)
dWx = (x.T).dot(dnext_h)
dx = dnext_h.dot(Wx.T)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return dx, dprev_h, dWx, dWh, db
def rnn_forward(x, h0, Wx, Wh, b):
"""
Run a vanilla RNN forward on an entire sequence of data. We assume an input
sequence composed of T vectors, each of dimension D. The RNN uses a hidden
size of H, and we work over a minibatch containing N sequences. After running
the RNN forward, we return the hidden states for all timesteps.
Inputs:
- x: Input data for the entire timeseries, of shape (N, T, D).
- h0: Initial hidden state, of shape (N, H)
- Wx: Weight matrix for input-to-hidden connections, of shape (D, H)
- Wh: Weight matrix for hidden-to-hidden connections, of shape (H, H)
- b: Biases of shape (H,)
Returns a tuple of:
- h: Hidden states for the entire timeseries, of shape (N, T, H).
- cache: Values needed in the backward pass
"""
h, cache = None, None
##############################################################################
# TODO: Implement forward pass for a vanilla RNN running on a sequence of #
# input data. You should use the rnn_step_forward function that you defined #
# above. You can use a for loop to help compute the forward pass. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N, T, D = x.shape
N, H = h0.shape
h = np.zeros((N, T, H))
hi = h0
cache = []
for i in range(T):
xi = x[:, i, :].reshape(N, D)
hi, cachei = rnn_step_forward(xi, hi, Wx, Wh, b)
h[:, i, :] = hi
cache.append(cachei)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return h, cache
def rnn_backward(dh, cache):
"""
Compute the backward pass for a vanilla RNN over an entire sequence of data.
Inputs:
- dh: Upstream gradients of all hidden states, of shape (N, T, H).
NOTE: 'dh' contains the upstream gradients produced by the
individual loss functions at each timestep, *not* the gradients
being passed between timesteps (which you'll have to compute yourself
by calling rnn_step_backward in a loop).
Returns a tuple of:
- dx: Gradient of inputs, of shape (N, T, D)
- dh0: Gradient of initial hidden state, of shape (N, H)
- dWx: Gradient of input-to-hidden weights, of shape (D, H)
- dWh: Gradient of hidden-to-hidden weights, of shape (H, H)
- db: Gradient of biases, of shape (H,)
"""
dx, dh0, dWx, dWh, db = None, None, None, None, None
##############################################################################
# TODO: Implement the backward pass for a vanilla RNN running an entire #
# sequence of data. You should use the rnn_step_backward function that you #
# defined above. You can use a for loop to help compute the backward pass. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N, T, H = dh.shape
dxl, dprev_h, dWx, dWh, db = rnn_step_backward(dh[:,T-1,:], cache[T-1])
_,D = dxl.shape
dx = np.zeros((N,T,D))
dx[:,T-1,:] = dxl
for i in range(T-2, -1, -1):
dxi, dprev_hi, dWxi, dWhi, dbi = rnn_step_backward(dh[:,i,:]+dprev_h, cache[i])
dx[:,i,:] = dxi
dprev_h = dprev_hi
dWx += dWxi
dWh += dWhi
db += dbi
dh0 = dprev_h
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return dx, dh0, dWx, dWh, db
def word_embedding_forward(x, W):
"""
Forward pass for word embeddings. We operate on minibatches of size N where
each sequence has length T. We assume a vocabulary of V words, assigning each
word to a vector of dimension D.
Inputs:
- x: Integer array of shape (N, T) giving indices of words. Each element idx
of x muxt be in the range 0 <= idx < V.
- W: Weight matrix of shape (V, D) giving word vectors for all words.
Returns a tuple of:
- out: Array of shape (N, T, D) giving word vectors for all input words.
- cache: Values needed for the backward pass
"""
out, cache = None, None
##############################################################################
# TODO: Implement the forward pass for word embeddings. #
# #
# HINT: This can be done in one line using NumPy's array indexing. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out = W[x]
cache = (x,W)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return out, cache
def word_embedding_backward(dout, cache):
"""
Backward pass for word embeddings. We cannot back-propagate into the words
since they are integers, so we only return gradient for the word embedding
matrix.
HINT: Look up the function np.add.at
Inputs:
- dout: Upstream gradients of shape (N, T, D)
- cache: Values from the forward pass
Returns:
- dW: Gradient of word embedding matrix, of shape (V, D).
"""
dW = None
##############################################################################
# TODO: Implement the backward pass for word embeddings. #
# #
# Note that words can appear more than once in a sequence. #
# HINT: Look up the function np.add.at #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x, W = cache
dW = np.zeros(W.shape)
np.add.at(dW, x, dout)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return dW
Use LSTM to Improve RNN
We find that the general implement of backward pass has a severe computational problem. Therefore, we use LSTM instead to do forward and backward pass. To gain insight into LSTM quickly, look at this gragh:
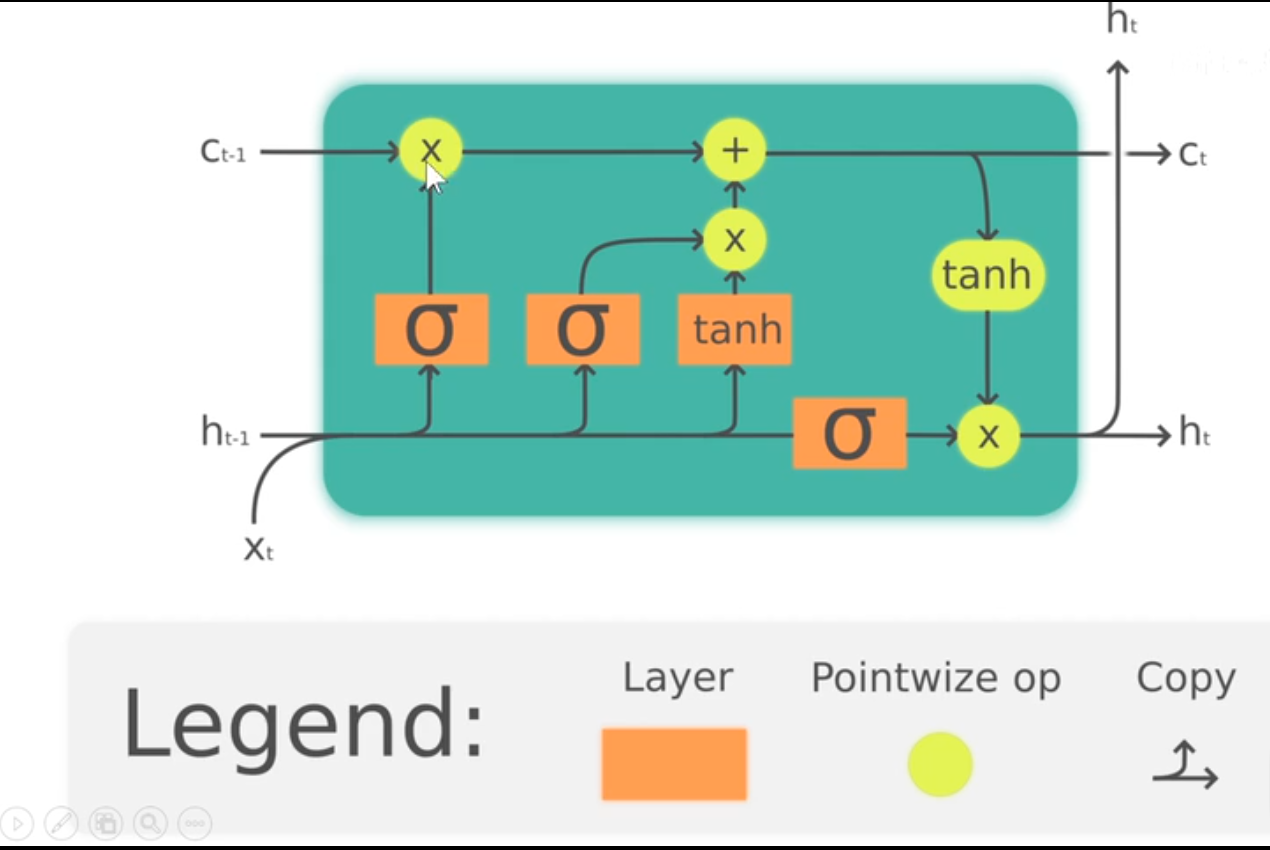
The mathmatical expression looks like this:
At each timestep we first compute an activation vector $a\in\mathbb{R}^{4H}$ as $a=W_xx_t + W_hh_{t-1}+b$. We then divide this into four vectors $a_i,a_f,a_o,a_g\in\mathbb{R}^H$ where $a_i$ consists of the first $H$ elements of $a$, $a_f$ is the next $H$ elements of $a$, etc. We then compute the input gate $g\in\mathbb{R}^H$, forget gate $f\in\mathbb{R}^H$, output gate $o\in\mathbb{R}^H$ and block input $g\in\mathbb{R}^H$ as
\[\begin{align*} i = \sigma(a_i) \hspace{2pc} f = \sigma(a_f) \hspace{2pc} o = \sigma(a_o) \hspace{2pc} g = \tanh(a_g) \end{align*}\]where $\sigma$ is the sigmoid function and $\tanh$ is the hyperbolic tangent, both applied elementwise.
Finally we compute the next cell state $c_t$ and next hidden state $h_t$ as
\[c_{t} = f\odot c_{t-1} + i\odot g \hspace{4pc} h_t = o\odot\tanh(c_t)\]where $\odot$ is the elementwise product of vectors.
Here I paste the key functions for the LSTM implement:
def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):
"""
Forward pass for a single timestep of an LSTM.
The input data has dimension D, the hidden state has dimension H, and we use
a minibatch size of N.
Note that a sigmoid() function has already been provided for you in this file.
Inputs:
- x: Input data, of shape (N, D)
- prev_h: Previous hidden state, of shape (N, H)
- prev_c: previous cell state, of shape (N, H)
- Wx: Input-to-hidden weights, of shape (D, 4H)
- Wh: Hidden-to-hidden weights, of shape (H, 4H)
- b: Biases, of shape (4H,)
Returns a tuple of:
- next_h: Next hidden state, of shape (N, H)
- next_c: Next cell state, of shape (N, H)
- cache: Tuple of values needed for backward pass.
"""
next_h, next_c, cache = None, None, None
#############################################################################
# TODO: Implement the forward pass for a single timestep of an LSTM. #
# You may want to use the numerically stable sigmoid implementation above. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
_,H = prev_h.shape
a = x.dot(Wx) + prev_h.dot(Wh) + b
i = sigmoid(a[:,0:H])
f = sigmoid(a[:,H:2*H])
o = sigmoid(a[:,2*H:3*H])
g = np.tanh(a[:,3*H:4*H])
next_c = f*prev_c + i*g
next_h = o*np.tanh(next_c)
cache = (next_c,i,f,o,g,x,prev_h,prev_c,Wh,Wx)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return next_h, next_c, cache
def lstm_step_backward(dnext_h, dnext_c, cache):
"""
Backward pass for a single timestep of an LSTM.
Inputs:
- dnext_h: Gradients of next hidden state, of shape (N, H)
- dnext_c: Gradients of next cell state, of shape (N, H)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient of input data, of shape (N, D)
- dprev_h: Gradient of previous hidden state, of shape (N, H)
- dprev_c: Gradient of previous cell state, of shape (N, H)
- dWx: Gradient of input-to-hidden weights, of shape (D, 4H)
- dWh: Gradient of hidden-to-hidden weights, of shape (H, 4H)
- db: Gradient of biases, of shape (4H,)
"""
dx, dprev_h, dprev_c, dWx, dWh, db = None, None, None, None, None, None
#############################################################################
# TODO: Implement the backward pass for a single timestep of an LSTM. #
# #
# HINT: For sigmoid and tanh you can compute local derivatives in terms of #
# the output value from the nonlinearity. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
next_c,i,f,o,g,x,prev_h,prev_c,Wh,Wx = cache
do = dnext_h*np.tanh(next_c)
dprev_c = (dnext_c + dnext_h*o*(1-np.tanh(next_c)**2))*f
df = (dnext_c + dnext_h*o*(1-np.tanh(next_c)**2))*prev_c
di = g*(dnext_c + dnext_h*o*(1-np.tanh(next_c)**2))
dg = i*(dnext_c + dnext_h*o*(1-np.tanh(next_c)**2))
dai = i*(1-i)*di
daf = f*(1-f)*df
dao = o*(1-o)*do
dag = (1-g**2)*dg
da = np.concatenate((dai,daf,dao,dag),axis = 1)
dx = da.dot(Wx.T)
dprev_h = da.dot(Wh.T)
dWx = x.T.dot(da)
dWh = prev_h.T.dot(da)
db = np.sum(da,axis = 0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return dx, dprev_h, dprev_c, dWx, dWh, db
def lstm_forward(x, h0, Wx, Wh, b):
"""
Forward pass for an LSTM over an entire sequence of data. We assume an input
sequence composed of T vectors, each of dimension D. The LSTM uses a hidden
size of H, and we work over a minibatch containing N sequences. After running
the LSTM forward, we return the hidden states for all timesteps.
Note that the initial cell state is passed as input, but the initial cell
state is set to zero. Also note that the cell state is not returned; it is
an internal variable to the LSTM and is not accessed from outside.
Inputs:
- x: Input data of shape (N, T, D)
- h0: Initial hidden state of shape (N, H)
- Wx: Weights for input-to-hidden connections, of shape (D, 4H)
- Wh: Weights for hidden-to-hidden connections, of shape (H, 4H)
- b: Biases of shape (4H,)
Returns a tuple of:
- h: Hidden states for all timesteps of all sequences, of shape (N, T, H)
- cache: Values needed for the backward pass.
"""
h, cache = None, None
#############################################################################
# TODO: Implement the forward pass for an LSTM over an entire timeseries. #
# You should use the lstm_step_forward function that you just defined. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N,T,D = x.shape
N,H = h0.shape
h = np.zeros((N,T,H))
hi = h0
ci = np.zeros_like(hi)
cache = []
for i in range(T):
xi = x[:,i,:].reshape(N,D)
hi,ci,cachei = lstm_step_forward(xi, hi, ci, Wx, Wh, b)
h[:,i,:] = hi
cache.append(cachei)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return h, cache
def lstm_backward(dh, cache):
"""
Backward pass for an LSTM over an entire sequence of data.]
Inputs:
- dh: Upstream gradients of hidden states, of shape (N, T, H)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient of input data of shape (N, T, D)
- dh0: Gradient of initial hidden state of shape (N, H)
- dWx: Gradient of input-to-hidden weight matrix of shape (D, 4H)
- dWh: Gradient of hidden-to-hidden weight matrix of shape (H, 4H)
- db: Gradient of biases, of shape (4H,)
"""
dx, dh0, dWx, dWh, db = None, None, None, None, None
#############################################################################
# TODO: Implement the backward pass for an LSTM over an entire timeseries. #
# You should use the lstm_step_backward function that you just defined. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N, T, H = dh.shape
dxl, dprev_h, dprev_c, dWx, dWh, db = lstm_step_backward(dh[:,T-1,:],np.zeros_like(dh[:,T-1,:]), cache[T-1])
_,D = dxl.shape
dx = np.zeros((N,T,D))
dx[:,T-1,:] = dxl
for i in range(T-2, -1, -1):
dxi, dprev_h, dprev_c, dWxi, dWhi, dbi = lstm_step_backward(dh[:,i,:]+dprev_h,dprev_c, cache[i])
dx[:,i,:] = dxi
dWx += dWxi
dWh += dWhi
db += dbi
dh0 = dprev_h
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return dx, dh0, dWx, dWh, db
Reference
min-char-rnn.py gist: 112 lines of Python