CS231n Assignments Note6: Implement Details of Training Models
Table of Contents:
- A Class Model for Implementing Networks
- A Solver Class as An API to Train Models
- Updating Rules
- Reference
A Class Model for Implementing Networks
Here I try to write a class model to help make sense of the general implement of different kinds of networks:
class Networks(object):
"""
A model for implementing all kinds of networks
"""
def __init__(self, input_dim, hidden_dim, num_classes, ..., hyperparameters, ...):
"""
Initialize a new network, including weights and bias.
"""
self.params = {}
"""
TODO: Weights should be initialized from a Gaussian centered at 0.0
with standard deviation equal to weight_scale; biases should be initialized to zero
"""
def loss(self, X, y=None):
"""
Evaluate loss and gradient for networks.
Inputs:
- X: Array of input data.
- y: Array of labels.
Returns:
If y is None, then run a test-time forward passand return scores.
If y is not None, then run a training-time forward and backward pass and return a tuple of:
- loss.
- grads.
"""
scores = None
scores = # forward pass
if y is None:
return scores
loss, grads = 0, {}
loss, dscore = # non-linearity loss function
grads = #backward pass
return loss, grads
A Solver Class as An API to Train Models
We train models using a separate class like this:
class Solver(object):
"""
A Solver encapsulates all the logic necessary for training classification
models. The Solver performs stochastic gradient descent using different
update rules defined in optim.py.
The solver accepts both training and validataion data and labels so it can
periodically check classification accuracy on both training and validation
data to watch out for overfitting.
To train a model, you will first construct a Solver instance, passing the
model, dataset, and various options (learning rate, batch size, etc) to the
constructor. You will then call the train() method to run the optimization
procedure and train the model.
After the train() method returns, model.params will contain the parameters
that performed best on the validation set over the course of training.
In addition, the instance variable solver.loss_history will contain a list
of all losses encountered during training and the instance variables
solver.train_acc_history and solver.val_acc_history will be lists of the
accuracies of the model on the training and validation set at each epoch.
Example usage might look something like this:
data = {
'X_train': # training data
'y_train': # training labels
'X_val': # validation data
'y_val': # validation labels
}
model = MyAwesomeModel(hidden_size=100, reg=10)
solver = Solver(model, data,
update_rule='sgd',
optim_config={
'learning_rate': 1e-3,
},
lr_decay=0.95,
num_epochs=10, batch_size=100,
print_every=100)
solver.train()
A Solver works on a model object that must conform to the following API:
- model.params must be a dictionary mapping string parameter names to numpy
arrays containing parameter values.
- model.loss(X, y) must be a function that computes training-time loss and
gradients, and test-time classification scores, with the following inputs
and outputs:
Inputs:
- X: Array giving a minibatch of input data of shape (N, d_1, ..., d_k)
- y: Array of labels, of shape (N,) giving labels for X where y[i] is the
label for X[i].
Returns:
If y is None, run a test-time forward pass and return:
- scores: Array of shape (N, C) giving classification scores for X where
scores[i, c] gives the score of class c for X[i].
If y is not None, run a training time forward and backward pass and
return a tuple of:
- loss: Scalar giving the loss
- grads: Dictionary with the same keys as self.params mapping parameter
names to gradients of the loss with respect to those parameters.
"""
def __init__(self, model, data, **kwargs):
"""
Construct a new Solver instance.
Required arguments:
- model: A model object conforming to the API described above
- data: A dictionary of training and validation data containing:
'X_train': Array, shape (N_train, d_1, ..., d_k) of training images
'X_val': Array, shape (N_val, d_1, ..., d_k) of validation images
'y_train': Array, shape (N_train,) of labels for training images
'y_val': Array, shape (N_val,) of labels for validation images
Optional arguments:
- update_rule: A string giving the name of an update rule in optim.py.
Default is 'sgd'.
- optim_config: A dictionary containing hyperparameters that will be
passed to the chosen update rule. Each update rule requires different
hyperparameters (see optim.py) but all update rules require a
'learning_rate' parameter so that should always be present.
- lr_decay: A scalar for learning rate decay; after each epoch the
learning rate is multiplied by this value.
- batch_size: Size of minibatches used to compute loss and gradient
during training.
- num_epochs: The number of epochs to run for during training.
- print_every: Integer; training losses will be printed every
print_every iterations.
- verbose: Boolean; if set to false then no output will be printed
during training.
- num_train_samples: Number of training samples used to check training
accuracy; default is 1000; set to None to use entire training set.
- num_val_samples: Number of validation samples to use to check val
accuracy; default is None, which uses the entire validation set.
- checkpoint_name: If not None, then save model checkpoints here every
epoch.
"""
self.model = model
self.X_train = data['X_train']
self.y_train = data['y_train']
self.X_val = data['X_val']
self.y_val = data['y_val']
# Unpack keyword arguments
self.update_rule = kwargs.pop('update_rule', 'sgd')
self.optim_config = kwargs.pop('optim_config', {})
self.lr_decay = kwargs.pop('lr_decay', 1.0)
self.batch_size = kwargs.pop('batch_size', 100)
self.num_epochs = kwargs.pop('num_epochs', 10)
self.num_train_samples = kwargs.pop('num_train_samples', 1000)
self.num_val_samples = kwargs.pop('num_val_samples', None)
self.checkpoint_name = kwargs.pop('checkpoint_name', None)
self.print_every = kwargs.pop('print_every', 10)
self.verbose = kwargs.pop('verbose', True)
# Throw an error if there are extra keyword arguments
if len(kwargs) > 0:
extra = ', '.join('"%s"' % k for k in list(kwargs.keys()))
raise ValueError('Unrecognized arguments %s' % extra)
# Make sure the update rule exists, then replace the string
# name with the actual function
if not hasattr(optim, self.update_rule):
raise ValueError('Invalid update_rule "%s"' % self.update_rule)
self.update_rule = getattr(optim, self.update_rule)
self._reset()
def _reset(self):
"""
Set up some book-keeping variables for optimization. Don't call this
manually.
"""
# Set up some variables for book-keeping
self.epoch = 0
self.best_val_acc = 0
self.best_params = {}
self.loss_history = []
self.train_acc_history = []
self.val_acc_history = []
# Make a deep copy of the optim_config for each parameter
self.optim_configs = {}
for p in self.model.params:
d = {k: v for k, v in self.optim_config.items()}
self.optim_configs[p] = d
def _step(self):
"""
Make a single gradient update. This is called by train() and should not
be called manually.
"""
# Make a minibatch of training data
num_train = self.X_train.shape[0]
batch_mask = np.random.choice(num_train, self.batch_size)
X_batch = self.X_train[batch_mask]
y_batch = self.y_train[batch_mask]
# Compute loss and gradient
loss, grads = self.model.loss(X_batch, y_batch)
self.loss_history.append(loss)
# Perform a parameter update
for p, w in self.model.params.items():
dw = grads[p]
config = self.optim_configs[p]
next_w, next_config = self.update_rule(w, dw, config)
self.model.params[p] = next_w
self.optim_configs[p] = next_config
def _save_checkpoint(self):
if self.checkpoint_name is None: return
checkpoint = {
'model': self.model,
'update_rule': self.update_rule,
'lr_decay': self.lr_decay,
'optim_config': self.optim_config,
'batch_size': self.batch_size,
'num_train_samples': self.num_train_samples,
'num_val_samples': self.num_val_samples,
'epoch': self.epoch,
'loss_history': self.loss_history,
'train_acc_history': self.train_acc_history,
'val_acc_history': self.val_acc_history,
}
filename = '%s_epoch_%d.pkl' % (self.checkpoint_name, self.epoch)
if self.verbose:
print('Saving checkpoint to "%s"' % filename)
with open(filename, 'wb') as f:
pickle.dump(checkpoint, f)
def check_accuracy(self, X, y, num_samples=None, batch_size=100):
"""
Check accuracy of the model on the provided data.
Inputs:
- X: Array of data, of shape (N, d_1, ..., d_k)
- y: Array of labels, of shape (N,)
- num_samples: If not None, subsample the data and only test the model
on num_samples datapoints.
- batch_size: Split X and y into batches of this size to avoid using
too much memory.
Returns:
- acc: Scalar giving the fraction of instances that were correctly
classified by the model.
"""
# Maybe subsample the data
N = X.shape[0]
if num_samples is not None and N > num_samples:
mask = np.random.choice(N, num_samples)
N = num_samples
X = X[mask]
y = y[mask]
# Compute predictions in batches
num_batches = N // batch_size
if N % batch_size != 0:
num_batches += 1
y_pred = []
for i in range(num_batches):
start = i * batch_size
end = (i + 1) * batch_size
scores = self.model.loss(X[start:end])
y_pred.append(np.argmax(scores, axis=1))
y_pred = np.hstack(y_pred)
acc = np.mean(y_pred == y)
return acc
def train(self):
"""
Run optimization to train the model.
"""
num_train = self.X_train.shape[0]
iterations_per_epoch = max(num_train // self.batch_size, 1)
num_iterations = self.num_epochs * iterations_per_epoch
for t in range(num_iterations):
self._step()
# Maybe print training loss
if self.verbose and t % self.print_every == 0:
print('(Iteration %d / %d) loss: %f' % (
t + 1, num_iterations, self.loss_history[-1]))
# At the end of every epoch, increment the epoch counter and decay
# the learning rate.
epoch_end = (t + 1) % iterations_per_epoch == 0
if epoch_end:
self.epoch += 1
for k in self.optim_configs:
self.optim_configs[k]['learning_rate'] *= self.lr_decay
# Check train and val accuracy on the first iteration, the last
# iteration, and at the end of each epoch.
first_it = (t == 0)
last_it = (t == num_iterations - 1)
if first_it or last_it or epoch_end:
train_acc = self.check_accuracy(self.X_train, self.y_train,
num_samples=self.num_train_samples)
val_acc = self.check_accuracy(self.X_val, self.y_val,
num_samples=self.num_val_samples)
self.train_acc_history.append(train_acc)
self.val_acc_history.append(val_acc)
self._save_checkpoint()
if self.verbose:
print('(Epoch %d / %d) train acc: %f; val_acc: %f' % (
self.epoch, self.num_epochs, train_acc, val_acc))
# Keep track of the best model
if val_acc > self.best_val_acc:
self.best_val_acc = val_acc
self.best_params = {}
for k, v in self.model.params.items():
self.best_params[k] = v.copy()
# At the end of training swap the best params into the model
self.model.params = self.best_params
Updating Rules
Removing details, we conclude that Adam and SGD+Momentum are currently recommended to use. Here I paste most used rules implement to optimize parameters:
import numpy as np
"""
This file implements various first-order update rules that are commonly used
for training neural networks. Each update rule accepts current weights and the
gradient of the loss with respect to those weights and produces the next set of
weights. Each update rule has the same interface:
def update(w, dw, config=None):
Inputs:
- w: A numpy array giving the current weights.
- dw: A numpy array of the same shape as w giving the gradient of the
loss with respect to w.
- config: A dictionary containing hyperparameter values such as learning
rate, momentum, etc. If the update rule requires caching values over many
iterations, then config will also hold these cached values.
Returns:
- next_w: The next point after the update.
- config: The config dictionary to be passed to the next iteration of the
update rule.
NOTE: For most update rules, the default learning rate will probably not
perform well; however the default values of the other hyperparameters should
work well for a variety of different problems.
For efficiency, update rules may perform in-place updates, mutating w and
setting next_w equal to w.
"""
def sgd(w, dw, config=None):
"""
Performs vanilla stochastic gradient descent.
config format:
- learning_rate: Scalar learning rate.
"""
if config is None: config = {}
config.setdefault('learning_rate', 1e-2)
w -= config['learning_rate'] * dw
return w, config
def sgd_momentum(w, dw, config=None):
"""
Performs stochastic gradient descent with momentum.
config format:
- learning_rate: Scalar learning rate.
- momentum: Scalar between 0 and 1 giving the momentum value.
Setting momentum = 0 reduces to sgd.
- velocity: A numpy array of the same shape as w and dw used to store a
moving average of the gradients.
"""
if config is None: config = {}
config.setdefault('learning_rate', 1e-2)
config.setdefault('momentum', 0.9)
v = config.get('velocity', np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the momentum update formula. Store the updated value in #
# the next_w variable. You should also use and update the velocity v. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
v = config['momentum'] * v - config['learning_rate'] * dw
next_w = w + v
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
config['velocity'] = v
return next_w, config
def rmsprop(w, dw, config=None):
"""
Uses the RMSProp update rule, which uses a moving average of squared
gradient values to set adaptive per-parameter learning rates.
config format:
- learning_rate: Scalar learning rate.
- decay_rate: Scalar between 0 and 1 giving the decay rate for the squared
gradient cache.
- epsilon: Small scalar used for smoothing to avoid dividing by zero.
- cache: Moving average of second moments of gradients.
"""
if config is None: config = {}
config.setdefault('learning_rate', 1e-2)
config.setdefault('decay_rate', 0.99)
config.setdefault('epsilon', 1e-8)
config.setdefault('cache', np.zeros_like(w))
next_w = None
###########################################################################
# TODO: Implement the RMSprop update formula, storing the next value of w #
# in the next_w variable. Don't forget to update cache value stored in #
# config['cache']. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
config['cache'] = config['decay_rate'] * config['cache'] + (1 - config['decay_rate']) * dw**2
next_w = w - config['learning_rate'] * dw / (np.sqrt(config['cache']) + config['epsilon'])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
def adam(w, dw, config=None):
"""
Uses the Adam update rule, which incorporates moving averages of both the
gradient and its square and a bias correction term.
config format:
- learning_rate: Scalar learning rate.
- beta1: Decay rate for moving average of first moment of gradient.
- beta2: Decay rate for moving average of second moment of gradient.
- epsilon: Small scalar used for smoothing to avoid dividing by zero.
- m: Moving average of gradient.
- v: Moving average of squared gradient.
- t: Iteration number.
"""
if config is None: config = {}
config.setdefault('learning_rate', 1e-3)
config.setdefault('beta1', 0.9)
config.setdefault('beta2', 0.999)
config.setdefault('epsilon', 1e-8)
config.setdefault('m', np.zeros_like(w))
config.setdefault('v', np.zeros_like(w))
config.setdefault('t', 0)
next_w = None
###########################################################################
# TODO: Implement the Adam update formula, storing the next value of w in #
# the next_w variable. Don't forget to update the m, v, and t variables #
# stored in config. #
# #
# NOTE: In order to match the reference output, please modify t _before_ #
# using it in any calculations. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
config['t'] += 1
config['m'] = config['beta1']*config['m'] + (1-config['beta1'])*dw
mt = config['m'] / (1-config['beta1']**config['t'])
config['v'] = config['beta2']*config['v'] + (1-config['beta2'])*(dw**2)
vt = config['v'] / (1-config['beta2']**config['t'])
next_w = w - config['learning_rate'] * mt / (np.sqrt(vt) + config['epsilon'])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return next_w, config
and a useful animation:
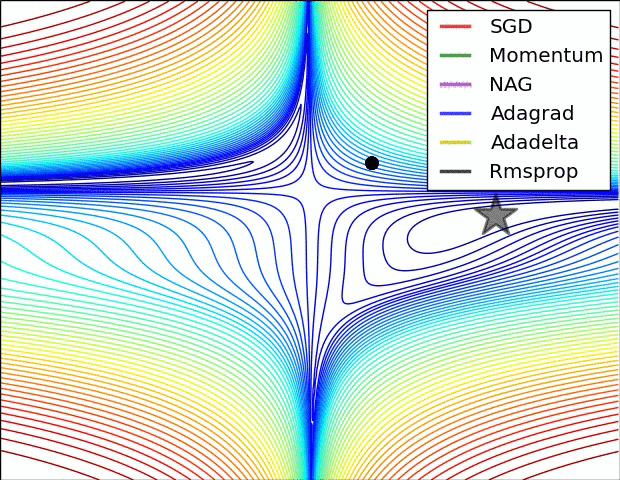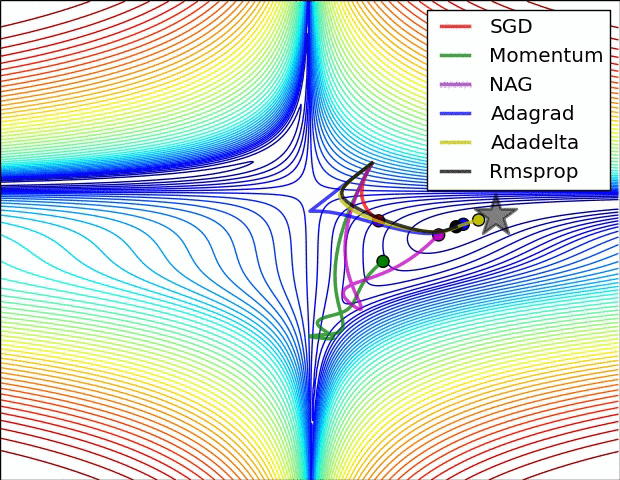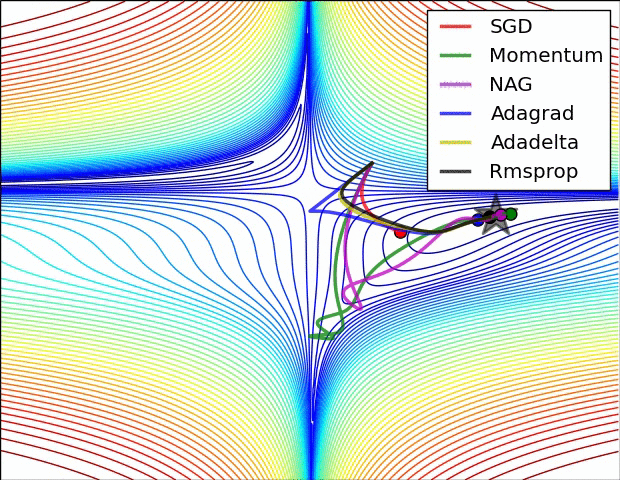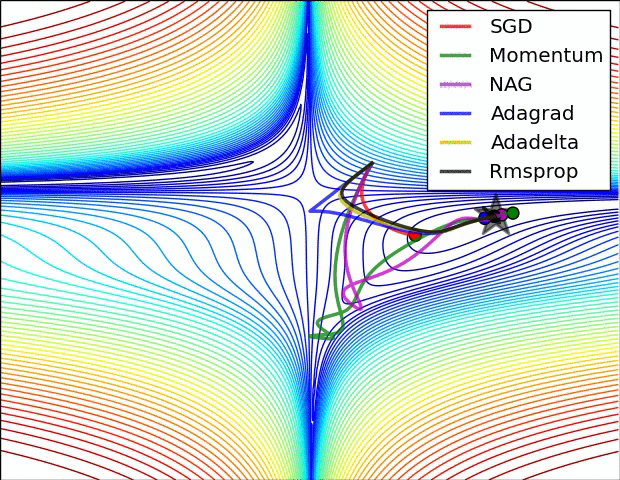
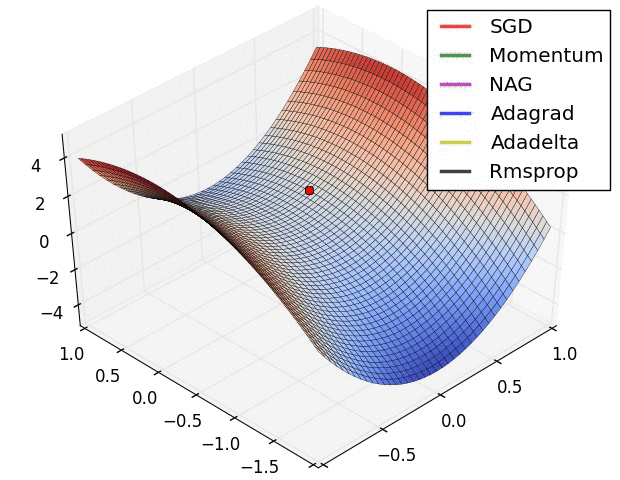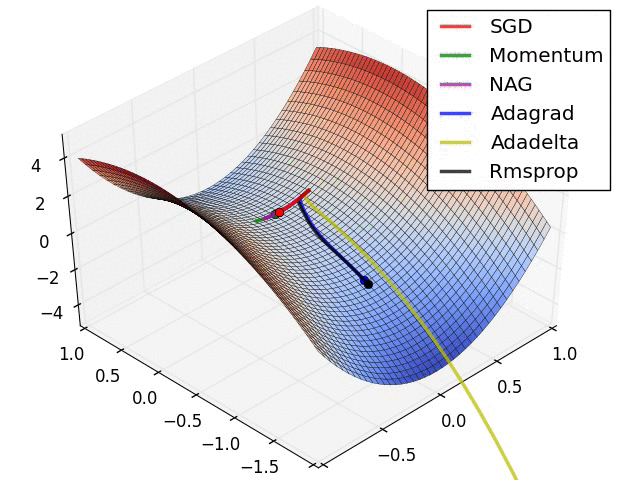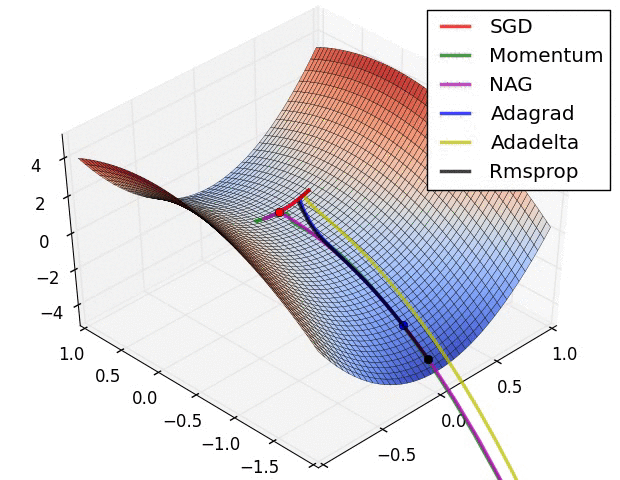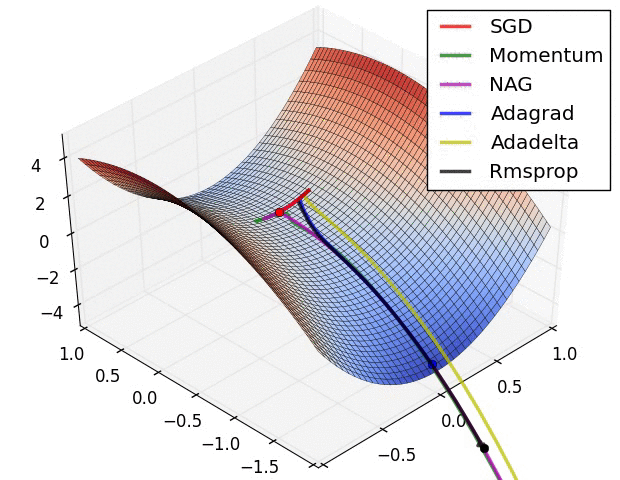
Animations that may help your intuitions about the learning process dynamics. Left: Contours of a loss surface and time evolution of different optimization algorithms. Notice the “overshooting” behavior of momentum-based methods, which make the optimization look like a ball rolling down the hill. Right: A visualization of a saddle point in the optimization landscape, where the curvature along different dimension has different signs (one dimension curves up and another down). Notice that SGD has a very hard time breaking symmetry and gets stuck on the top. Conversely, algorithms such as RMSprop will see very low gradients in the saddle direction. Due to the denominator term in the RMSprop update, this will increase the effective learning rate along this direction, helping RMSProp proceed. Images credit: Alec Radford.
Reference
Neural Networks Part 3: Learning and Evaluation
Assignment #2: Fully-Connected Nets, Batch Normalization, Dropout, Convolutional Nets