CS231n Assignments Note4: Fully-Connected Neural Network
- A Try to Interpret the Architecture of A Fully Connected Neural Network
- Batch Normalization
- Dropout
- A Bunch of Commonly Used Layers
- Reference
A Try to Interpret the Architecture of A Fully Connected Neural Network
It is much simpler to implement a neural network with modular method like stack a Lego Bricks. Concretely, we can implement different layer types in isolation and then snap them together into models with different kinds of architectures.
For each layer we will implement a forward and a backward function. The forward function will receive inputs, weights, and other parameters and will return both an output and a `cache object storing data needed for the backward pass, like this:
def layer_forward(x, w):
""" Receive inputs x and weights w """
# Do some computations ...
z = # ... some intermediate value
# Do some more computations ...
out = # the output
cache = (x, w, z, out) # Values we need to compute gradients
return out, cache
The backward pass will receive upstream derivatives and the cache object, and will return gradients with respect to the inputs and weights, like this:
def layer_backward(dout, cache):
"""
Receive dout (derivative of loss with respect to outputs) and cache,
and compute derivative with respect to inputs.
"""
# Unpack cache values
x, w, z, out = cache
# use values in cache to compute derivatives
dx = # Derivative of loss with respect to x
dw = # Derivative of loss with respect to w
return dx, dw
After implementing a bunch of layers this way, we will be able to easily combine the to build classifiers with different architectures.
Batch Normalization
To make deep network easier to train, we can use a strategy of batch normalization to change the architecture of the network.
It works better when input data consist of uncorrelated features with zero mean and unit variance. But the shifting distribution of features inside deep neural networks may make training deep networks more difficult.
Concretely, to overcome this problem, we insert batch normalization layers into the network, that is to say, append a batch normalization layer immediately after fully-connected layers or convolutional layers, and before non-linearities.
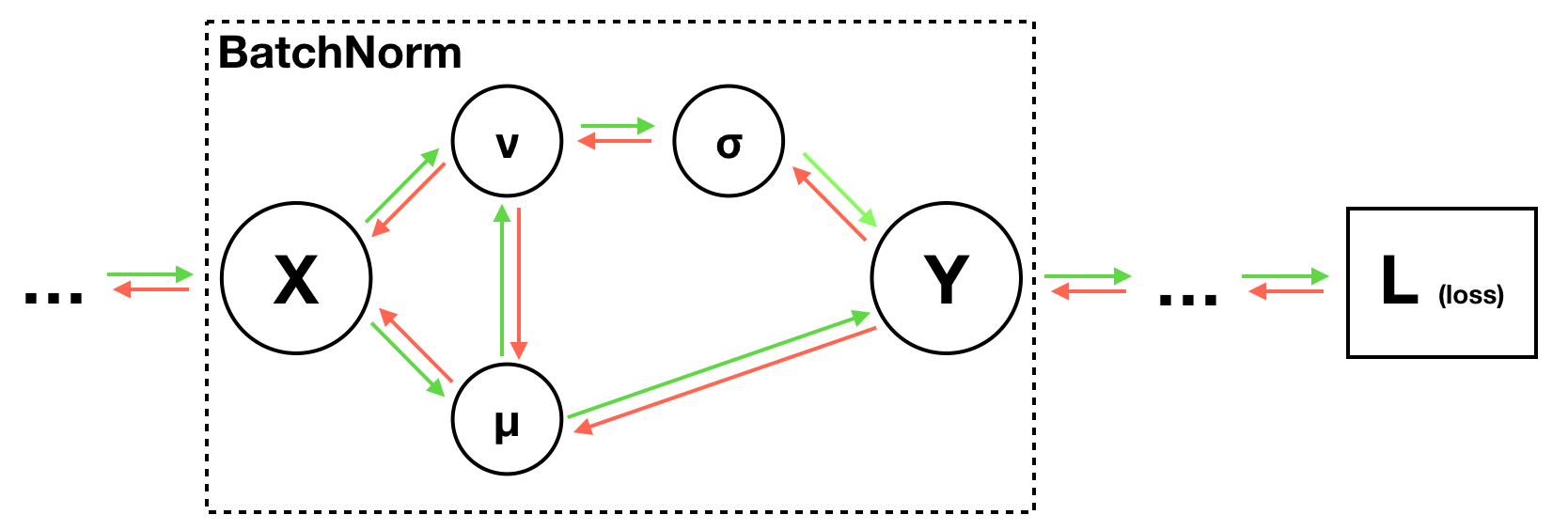
Layer Normalization is proposed to improve batch normalization
Dropout
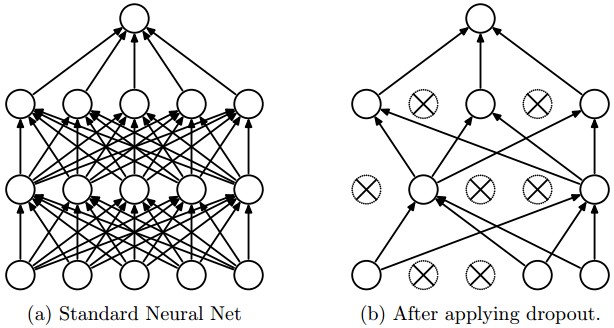
Figure taken from the Dropout paper that illustrates the idea. During training, Dropout can be interpreted as sampling a Neural Network within the full Neural Network, and only updating the parameters of the sampled network based on the input data. (However, the exponential number of possible sampled networks are not independent because they share the parameters.) During testing there is no dropout applied, with the interpretation of evaluating an averaged prediction across the exponentially-sized ensemble of all sub-networks (more about ensembles in the next section).
Dropout is a technique for regularizing neural networks by randomly setting some output activations to zero during the forward pass.
A Bunch of Commonly Used Layers
Here I list the implement of some useful layers:
def affine_forward(x, w, b):
"""
Computes the forward pass for an affine (fully-connected) layer.
The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
examples, where each example x[i] has shape (d_1, ..., d_k). We will
reshape each input into a vector of dimension D = d_1 * ... * d_k, and
then transform it to an output vector of dimension M.
Inputs:
- x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
- w: A numpy array of weights, of shape (D, M)
- b: A numpy array of biases, of shape (M,)
Returns a tuple of:
- out: output, of shape (N, M)
- cache: (x, w, b)
"""
out = None
###########################################################################
# TODO: Implement the affine forward pass. Store the result in out. You #
# will need to reshape the input into rows. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N = x.shape[0]
D = w.shape[0]
out = x.reshape(N, D).dot(w) + b
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, w, b)
return out, cache
def affine_backward(dout, cache):
"""
Computes the backward pass for an affine layer.
Inputs:
- dout: Upstream derivative, of shape (N, M)
- cache: Tuple of:
- x: Input data, of shape (N, d_1, ... d_k)
- w: Weights, of shape (D, M)
- b: Biases, of shape (M,)
Returns a tuple of:
- dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
- dw: Gradient with respect to w, of shape (D, M)
- db: Gradient with respect to b, of shape (M,)
"""
x, w, b = cache
dx, dw, db = None, None, None
###########################################################################
# TODO: Implement the affine backward pass. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
D, M = w.shape
N = x.shape[0]
db = np.sum(dout, axis=0)
dw = x.reshape(N, D).T.dot(dout)
dx = dout.dot(w.T).reshape(x.shape)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dw, db
def relu_forward(x):
"""
Computes the forward pass for a layer of rectified linear units (ReLUs).
Input:
- x: Inputs, of any shape
Returns a tuple of:
- out: Output, of the same shape as x
- cache: x
"""
out = None
###########################################################################
# TODO: Implement the ReLU forward pass. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out = np.maximum(0, x)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = x
return out, cache
def relu_backward(dout, cache):
"""
Computes the backward pass for a layer of rectified linear units (ReLUs).
Input:
- dout: Upstream derivatives, of any shape
- cache: Input x, of same shape as dout
Returns:
- dx: Gradient with respect to x
"""
dx, x = None, cache
###########################################################################
# TODO: Implement the ReLU backward pass. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dx = np.ones(x.shape)
dx[x<=0] = 0
dx *= dout
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx
def batchnorm_forward(x, gamma, beta, bn_param):
"""
Forward pass for batch normalization.
During training the sample mean and (uncorrected) sample variance are
computed from minibatch statistics and used to normalize the incoming data.
During training we also keep an exponentially decaying running mean of the
mean and variance of each feature, and these averages are used to normalize
data at test-time.
At each timestep we update the running averages for mean and variance using
an exponential decay based on the momentum parameter:
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
Note that the batch normalization paper suggests a different test-time
behavior: they compute sample mean and variance for each feature using a
large number of training images rather than using a running average. For
this implementation we have chosen to use running averages instead since
they do not require an additional estimation step; the torch7
implementation of batch normalization also uses running averages.
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
#######################################################################
# TODO: Implement the training-time forward pass for batch norm. #
# Use minibatch statistics to compute the mean and variance, use #
# these statistics to normalize the incoming data, and scale and #
# shift the normalized data using gamma and beta. #
# #
# You should store the output in the variable out. Any intermediates #
# that you need for the backward pass should be stored in the cache #
# variable. #
# #
# You should also use your computed sample mean and variance together #
# with the momentum variable to update the running mean and running #
# variance, storing your result in the running_mean and running_var #
# variables. #
# #
# Note that though you should be keeping track of the running #
# variance, you should normalize the data based on the standard #
# deviation (square root of variance) instead! #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
mu = np.mean(x,axis = 0)
num = x-mu
square_mu = num**2
var = np.mean(square_mu,axis = 0)
sqrtvar = np.sqrt(var + eps)
inverse_var = 1/sqrtvar
norm = num*inverse_var
scale_norm = gamma*norm
shift_norm = scale_norm + beta
out = shift_norm
running_mean = momentum * running_mean + (1 - momentum) * mu
running_var = momentum * running_var + (1 - momentum) * var
cache = (beta,gamma,norm,num,var,eps,sqrtvar)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
#######################################################################
# TODO: Implement the test-time forward pass for batch normalization. #
# Use the running mean and variance to normalize the incoming data, #
# then scale and shift the normalized data using gamma and beta. #
# Store the result in the out variable. #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out_hat = (x-running_mean)/(np.sqrt(running_var)+eps)
out = gamma*out_hat + beta
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
def batchnorm_backward(dout, cache):
"""
Backward pass for batch normalization.
For this implementation, you should write out a computation graph for
batch normalization on paper and propagate gradients backward through
intermediate nodes.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from batchnorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# Referencing the original paper (https://arxiv.org/abs/1502.03167) #
# might prove to be helpful. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
beta,gamma,norm,num,var,eps,sqrtvar = cache
N = dout.shape[0]
dbeta = np.sum(dout,axis = 0)
dgamma = np.sum(dout*norm,axis = 0)
dscale_norm = dout*gamma
dnorm_up = 1/np.sqrt(var + eps)*dscale_norm
#down branch
dnorm_down = np.sum(num*dscale_norm,axis = 0)
dinverse_var = dnorm_down*-1/(np.sqrt(var + eps))**2
dsqrtvar = 0.5/np.sqrt(var + eps)*dinverse_var
dvar = np.ones(dout.shape)*dsqrtvar/N
dsquare_mu = 2*num*dvar
dnum = dsquare_mu+dnorm_up
dmu = 1/N*np.ones(dout.shape)*-np.sum(dnum,axis = 0)
dx = dnum + dmu
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
def batchnorm_backward_alt(dout, cache):
"""
Alternative backward pass for batch normalization.
For this implementation you should work out the derivatives for the batch
normalizaton backward pass on paper and simplify as much as possible. You
should be able to derive a simple expression for the backward pass.
See the jupyter notebook for more hints.
Note: This implementation should expect to receive the same cache variable
as batchnorm_backward, but might not use all of the values in the cache.
Inputs / outputs: Same as batchnorm_backward
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for batch normalization. Store the #
# results in the dx, dgamma, and dbeta variables. #
# #
# After computing the gradient with respect to the centered inputs, you #
# should be able to compute gradients with respect to the inputs in a #
# single statement; our implementation fits on a single 80-character line.#
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
beta,gamma,norm,num,var,eps,sqrtvar = cache
N = dout.shape[0]
dbeta = np.sum(dout,axis = 0)
dgamma = np.sum(dout*norm,axis = 0)
dmu = np.sum(dout, axis=0)/N
dvar = 2/N * np.sum(num*dout, axis=0)
dstd= dvar/(2*sqrtvar)
dx = gamma*((dout - dmu)*sqrtvar - dstd*(num))/sqrtvar**2
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
def layernorm_forward(x, gamma, beta, ln_param):
"""
Forward pass for layer normalization.
During both training and test-time, the incoming data is normalized per data-point,
before being scaled by gamma and beta parameters identical to that of batch normalization.
Note that in contrast to batch normalization, the behavior during train and test-time for
layer normalization are identical, and we do not need to keep track of running averages
of any sort.
Input:
- x: Data of shape (N, D)
- gamma: Scale parameter of shape (D,)
- beta: Shift paremeter of shape (D,)
- ln_param: Dictionary with the following keys:
- eps: Constant for numeric stability
Returns a tuple of:
- out: of shape (N, D)
- cache: A tuple of values needed in the backward pass
"""
out, cache = None, None
eps = ln_param.get('eps', 1e-5)
###########################################################################
# TODO: Implement the training-time forward pass for layer norm. #
# Normalize the incoming data, and scale and shift the normalized data #
# using gamma and beta. #
# HINT: this can be done by slightly modifying your training-time #
# implementation of batch normalization, and inserting a line or two of #
# well-placed code. In particular, can you think of any matrix #
# transformations you could perform, that would enable you to copy over #
# the batch norm code and leave it almost unchanged? #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x = x.T
mu = np.mean(x,axis = 0)
num = x-mu
#denom-
square_mu = num**2
var = np.mean(square_mu,axis = 0)
sqrtvar = np.sqrt(var + eps)
inverse_var = 1/sqrtvar
norm = num*inverse_var
norm = norm.T
scale_norm = gamma*norm
shift_norm = scale_norm + beta
out = shift_norm
cache = (beta,gamma,norm,num,var,eps,sqrtvar)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return out, cache
def layernorm_backward(dout, cache):
"""
Backward pass for layer normalization.
For this implementation, you can heavily rely on the work you've done already
for batch normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, D)
- cache: Variable of intermediates from layernorm_forward.
Returns a tuple of:
- dx: Gradient with respect to inputs x, of shape (N, D)
- dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
- dbeta: Gradient with respect to shift parameter beta, of shape (D,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for layer norm. #
# #
# HINT: this can be done by slightly modifying your training-time #
# implementation of batch normalization. The hints to the forward pass #
# still apply! #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
beta,gamma,norm,num,var,eps,std = cache
_,D = dout.shape
dbeta = np.sum(dout,axis = 0)
dgamma = np.sum(dout*norm,axis = 0)
dout = dout.T
dscale_norm = gamma.reshape(dout.shape[0],1)*dout
dnorm_up = 1/np.sqrt(var + eps)*dscale_norm
#down branch
dnorm_down = np.sum(num*dscale_norm,axis = 0)
dinverse_var = dnorm_down*-1/(np.sqrt(var + eps))**2
dsqrtvar = 0.5/np.sqrt(var + eps)*dinverse_var
dvar = np.ones(dout.shape)*dsqrtvar/D
dsquare_mu = 2*num*dvar
dnum = dsquare_mu+dnorm_up
dmu = 1/D*np.ones(dout.shape)*-np.sum(dnum,axis = 0)
dx = dnum + dmu
dx = dx.T
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
def dropout_forward(x, dropout_param):
"""
Performs the forward pass for (inverted) dropout.
Inputs:
- x: Input data, of any shape
- dropout_param: A dictionary with the following keys:
- p: Dropout parameter. We keep each neuron output with probability p.
- mode: 'test' or 'train'. If the mode is train, then perform dropout;
if the mode is test, then just return the input.
- seed: Seed for the random number generator. Passing seed makes this
function deterministic, which is needed for gradient checking but not
in real networks.
Outputs:
- out: Array of the same shape as x.
- cache: tuple (dropout_param, mask). In training mode, mask is the dropout
mask that was used to multiply the input; in test mode, mask is None.
NOTE: Please implement **inverted** dropout, not the vanilla version of dropout.
See http://cs231n.github.io/neural-networks-2/#reg for more details.
NOTE 2: Keep in mind that p is the probability of **keep** a neuron
output; this might be contrary to some sources, where it is referred to
as the probability of dropping a neuron output.
"""
p, mode = dropout_param['p'], dropout_param['mode']
if 'seed' in dropout_param:
np.random.seed(dropout_param['seed'])
mask = None
out = None
if mode == 'train':
#######################################################################
# TODO: Implement training phase forward pass for inverted dropout. #
# Store the dropout mask in the mask variable. #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
p = dropout_param['p']
mask = (np.random.rand(*x.shape) < p) / p
out = x * mask
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
#######################################################################
# TODO: Implement the test phase forward pass for inverted dropout. #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out = x
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
cache = (dropout_param, mask)
out = out.astype(x.dtype, copy=False)
return out, cache
def dropout_backward(dout, cache):
"""
Perform the backward pass for (inverted) dropout.
Inputs:
- dout: Upstream derivatives, of any shape
- cache: (dropout_param, mask) from dropout_forward.
"""
dropout_param, mask = cache
mode = dropout_param['mode']
dx = None
if mode == 'train':
#######################################################################
# TODO: Implement training phase backward pass for inverted dropout #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dx = dout * mask
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
#######################################################################
# END OF YOUR CODE #
#######################################################################
elif mode == 'test':
dx = dout
return dx
def conv_forward_naive(x, w, b, conv_param):
"""
A naive implementation of the forward pass for a convolutional layer.
The input consists of N data points, each with C channels, height H and
width W. We convolve each input with F different filters, where each filter
spans all C channels and has height HH and width WW.
Input:
- x: Input data of shape (N, C, H, W)
- w: Filter weights of shape (F, C, HH, WW)
- b: Biases, of shape (F,)
- conv_param: A dictionary with the following keys:
- 'stride': The number of pixels between adjacent receptive fields in the
horizontal and vertical directions.
- 'pad': The number of pixels that will be used to zero-pad the input.
During padding, 'pad' zeros should be placed symmetrically (i.e equally on both sides)
along the height and width axes of the input. Be careful not to modfiy the original
input x directly.
Returns a tuple of:
- out: Output data, of shape (N, F, H', W') where H' and W' are given by
H' = 1 + (H + 2 * pad - HH) / stride
W' = 1 + (W + 2 * pad - WW) / stride
- cache: (x, w, b, conv_param)
"""
out = None
###########################################################################
# TODO: Implement the convolutional forward pass. #
# Hint: you can use the function np.pad for padding. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
stride = conv_param['stride']
pad = conv_param['pad']
N,C,H,W = x.shape
F,C,HH,WW = w.shape
H_n = int(1 + (H + 2 * pad - HH) / stride)
W_n = int(1 + (W + 2 * pad - WW) / stride)
X_pad = np.pad(x,((0,0),(0,0),(pad,pad),(pad,pad)),'constant', constant_values=0)
out = np.zeros((N,F,H_n,W_n))
for i in range(N):
for j in range(H_n):
for k in range(W_n):
for f in range(F):
X_i = X_pad[i]
inp_con = X_i[:,j*stride:j*stride+HH,k*stride:k*stride+WW]
out_con = (inp_con*w[f,:,:,:]).sum() + b[f]
out[i,f,j,k] = out_con
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, w, b, conv_param)
return out, cache
def conv_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a convolutional layer.
Inputs:
- dout: Upstream derivatives.
- cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive
Returns a tuple of:
- dx: Gradient with respect to x
- dw: Gradient with respect to w
- db: Gradient with respect to b
"""
dx, dw, db = None, None, None
###########################################################################
# TODO: Implement the convolutional backward pass. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x, w, b, conv_param = cache
N, C, H, W = x.shape
F, C, HH, WW = w.shape
stride = conv_param['stride']
pad = conv_param['pad']
x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant', constant_values=0)
H_n = 1 + (H + 2 * pad - HH) // stride
W_n = 1 + (W + 2 * pad - WW) // stride
dx_pad = np.zeros_like(x_pad)
dx = np.zeros_like(x)
dw = np.zeros_like(w)
db = np.zeros_like(b)
for n in range(N):
for f in range(F):
db[f] += dout[n, f].sum()
for j in range(0, H_n):
for i in range(0, W_n):
dw[f] += x_pad[n,:,j*stride:j*stride+HH,i*stride:i*stride+WW]*dout[n,f,j,i]
dx_pad[n,:,j*stride:j*stride+HH,i*stride:i*stride+WW] += w[f]*dout[n, f, j, i]
dx = dx_pad[:,:,pad:pad+H,pad:pad+W]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dw, db
def max_pool_forward_naive(x, pool_param):
"""
A naive implementation of the forward pass for a max-pooling layer.
Inputs:
- x: Input data, of shape (N, C, H, W)
- pool_param: dictionary with the following keys:
- 'pool_height': The height of each pooling region
- 'pool_width': The width of each pooling region
- 'stride': The distance between adjacent pooling regions
No padding is necessary here. Output size is given by
Returns a tuple of:
- out: Output data, of shape (N, C, H', W') where H' and W' are given by
H' = 1 + (H - pool_height) / stride
W' = 1 + (W - pool_width) / stride
- cache: (x, pool_param)
"""
out = None
###########################################################################
# TODO: Implement the max-pooling forward pass #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N, C, H, W = x.shape
pool_height = pool_param['pool_height']
pool_width = pool_param['pool_width']
stride = pool_param['stride']
H_n = int(1 + (H - pool_height) / stride)
W_n = int(1 + (W - pool_width) / stride)
out = np.zeros((N,C,H_n,W_n))
for i in range(N):
for j in range(H_n):
for k in range(W_n):
for l in range(C):
x_max = x[i,l,stride*j:stride*j+pool_height,stride*k:stride*k+pool_width]
out[i,l,j,k] = np.amax(x_max)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
cache = (x, pool_param)
return out, cache
def max_pool_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a max-pooling layer.
Inputs:
- dout: Upstream derivatives
- cache: A tuple of (x, pool_param) as in the forward pass.
Returns:
- dx: Gradient with respect to x
"""
dx = None
###########################################################################
# TODO: Implement the max-pooling backward pass #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x,pool_param = cache
N, C, H, W = x.shape
pool_height = pool_param['pool_height']
pool_width = pool_param['pool_width']
stride = pool_param['stride']
H_n = int(1 + (H - pool_height) / stride)
W_n = int(1 + (W - pool_width) / stride)
dx = np.zeros_like(x)
for i in range(N):
for j in range(H_n):
for k in range(W_n):
for l in range(C):
index = np.argmax(x[i,l,stride*j:stride*j+pool_height,stride*k:stride*k+pool_width])
ind1,ind2 = np.unravel_index(index,(pool_height, pool_width))
dx[i,l,stride*j:stride*j+pool_height,stride*k:stride*k+pool_width][ind1,ind2] = dout[i,l,j,k]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx
def spatial_batchnorm_forward(x, gamma, beta, bn_param):
"""
Computes the forward pass for spatial batch normalization.
Inputs:
- x: Input data of shape (N, C, H, W)
- gamma: Scale parameter, of shape (C,)
- beta: Shift parameter, of shape (C,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance. momentum=0 means that
old information is discarded completely at every time step, while
momentum=1 means that new information is never incorporated. The
default of momentum=0.9 should work well in most situations.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: Output data, of shape (N, C, H, W)
- cache: Values needed for the backward pass
"""
out, cache = None, None
###########################################################################
# TODO: Implement the forward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization by calling the #
# vanilla version of batch normalization you implemented above. #
# Your implementation should be very short; ours is less than five lines. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
_,C,_,_ = x.shape
running_mean = bn_param.get('running_mean', np.zeros((1,C,1,1), dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros((1,C,1,1), dtype=x.dtype))
if mode == 'train':
mu = np.mean(x,axis = (0,2,3),keepdims = True)
num = x-mu
#denom-
square_mu = num**2
var = np.mean(square_mu,axis = (0,2,3),keepdims = True)
sqrtvar = np.sqrt(var + eps)
inverse_var = 1/sqrtvar
norm = num*inverse_var
gamma = gamma.reshape(1,C,1,1)
beta = beta.reshape(1,C,1,1)
scale_norm = gamma*norm
shift_norm = scale_norm + beta
out = shift_norm
running_mean = momentum * running_mean + (1 - momentum) * mu
running_var = momentum * running_var + (1 - momentum) * var
cache = (beta,gamma,norm,num,var,eps,sqrtvar)
elif mode == 'test':
out_hat = (x-running_mean)/np.sqrt(running_var+eps)
out = gamma.reshape(1,C,1,1)*out_hat + beta.reshape(1,C,1,1)
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return out, cache
def spatial_batchnorm_backward(dout, cache):
"""
Computes the backward pass for spatial batch normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, C, H, W)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization by calling the #
# vanilla version of batch normalization you implemented above. #
# Your implementation should be very short; ours is less than five lines. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
beta,gamma,norm,num,var,eps,sqrtvar = cache
N,C,H,W = dout.shape
dbeta = np.sum(dout,axis = (0,2,3))
dgamma = np.sum(dout*norm,axis = (0,2,3))
dmu = np.mean(dout, axis=(0,2,3),keepdims = True)
dvar = 2 * np.mean(num*dout, axis=(0,2,3),keepdims = True)
dstd= dvar/(2*sqrtvar)
dx = gamma.reshape(1,C,1,1)*((dout - dmu)*sqrtvar - dstd*(num))/sqrtvar**2
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
def spatial_groupnorm_forward(x, gamma, beta, G, gn_param):
"""
Computes the forward pass for spatial group normalization.
In contrast to layer normalization, group normalization splits each entry
in the data into G contiguous pieces, which it then normalizes independently.
Per feature shifting and scaling are then applied to the data, in a manner identical to that of batch normalization and layer normalization.
Inputs:
- x: Input data of shape (N, C, H, W)
- gamma: Scale parameter, of shape (C,)
- beta: Shift parameter, of shape (C,)
- G: Integer mumber of groups to split into, should be a divisor of C
- gn_param: Dictionary with the following keys:
- eps: Constant for numeric stability
Returns a tuple of:
- out: Output data, of shape (N, C, H, W)
- cache: Values needed for the backward pass
"""
out, cache = None, None
eps = gn_param.get('eps',1e-5)
###########################################################################
# TODO: Implement the forward pass for spatial group normalization. #
# This will be extremely similar to the layer norm implementation. #
# In particular, think about how you could transform the matrix so that #
# the bulk of the code is similar to both train-time batch normalization #
# and layer normalization! #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
N,C,H,W = x.shape
x = x.reshape(N,G,C//G,H,W)
mu = np.mean(x,axis = (2,3,4),keepdims = True)
num = x-mu
#denom-
square_mu = num**2
var = np.mean(square_mu,axis = (2,3,4),keepdims = True)
sqrtvar = np.sqrt(var + eps)
inverse_var = 1/sqrtvar
norm = num*inverse_var
norm = norm.reshape(N,C,H,W)
gamma = gamma.reshape(1,C,1,1)
beta = beta.reshape(1,C,1,1)
scale_norm = gamma*norm
shift_norm = scale_norm + beta
out = shift_norm
cache = (beta,gamma,norm,num,var,eps,sqrtvar,G)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return out, cache
def spatial_groupnorm_backward(dout, cache):
"""
Computes the backward pass for spatial group normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, C, H, W)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for spatial group normalization. #
# This will be extremely similar to the layer norm implementation. #
###########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
beta,gamma,norm,num,var,eps,sqrtvar,G = cache
N,C,H,W = dout.shape
dbeta = np.sum(dout,axis = (0,2,3),keepdims=True)
dgamma = np.sum(dout*norm,axis = (0,2,3),keepdims=True)
dout = (gamma*dout).reshape(N,G,C//G,H,W)
dmu = np.mean(dout, axis=(2,3,4),keepdims = True)
dvar = 2 * np.mean(num*dout, axis=(2,3,4),keepdims = True)
dstd= dvar/(2*sqrtvar)
dx_before = ((dout - dmu)*sqrtvar - dstd*(num))/sqrtvar**2
dx = dx_before.reshape(N,C,H,W)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
def svm_loss(x, y):
"""
Computes the loss and gradient using for multiclass SVM classification.
Inputs:
- x: Input data, of shape (N, C) where x[i, j] is the score for the jth
class for the ith input.
- y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
0 <= y[i] < C
Returns a tuple of:
- loss: Scalar giving the loss
- dx: Gradient of the loss with respect to x
"""
N = x.shape[0]
correct_class_scores = x[np.arange(N), y]
margins = np.maximum(0, x - correct_class_scores[:, np.newaxis] + 1.0)
margins[np.arange(N), y] = 0
loss = np.sum(margins) / N
num_pos = np.sum(margins > 0, axis=1)
dx = np.zeros_like(x)
dx[margins > 0] = 1
dx[np.arange(N), y] -= num_pos
dx /= N
return loss, dx
def softmax_loss(x, y):
"""
Computes the loss and gradient for softmax classification.
Inputs:
- x: Input data, of shape (N, C) where x[i, j] is the score for the jth
class for the ith input.
- y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
0 <= y[i] < C
Returns a tuple of:
- loss: Scalar giving the loss
- dx: Gradient of the loss with respect to x
"""
shifted_logits = x - np.max(x, axis=1, keepdims=True)
Z = np.sum(np.exp(shifted_logits), axis=1, keepdims=True)
log_probs = shifted_logits - np.log(Z)
probs = np.exp(log_probs)
N = x.shape[0]
loss = -np.sum(log_probs[np.arange(N), y]) / N
dx = probs.copy()
dx[np.arange(N), y] -= 1
dx /= N
return loss, dx
Reference
Neural Networks Part 2: Setting up the Data and the Loss
Assignment #2: Fully-Connected Nets, Batch Normalization, Dropout, Convolutional Nets