CS231n Assignments Note3: Two Layer Neural Network
- A Try to Interpret How Neural Network Works
- Debug the Training and Tuning the Hyperparameters
- Reference
A Try to Interpret How Neural Network Works
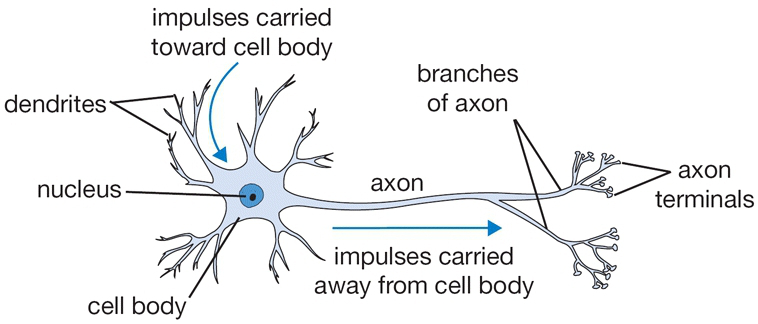
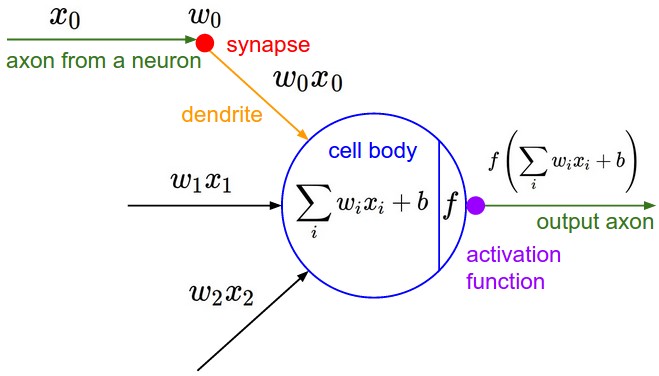
A cartoon drawing of a biological neuron (left) and its mathematical model (right).
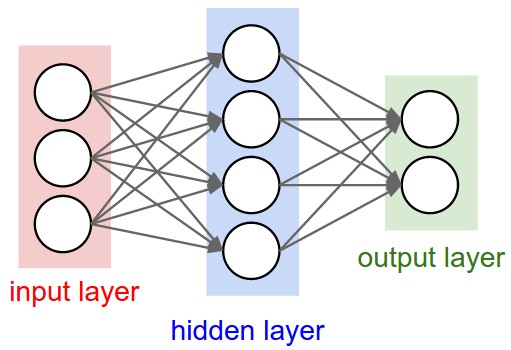
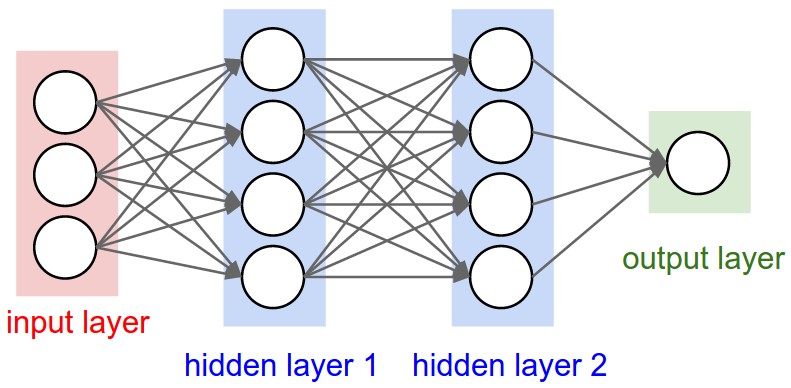
Left: A 2-layer Neural Network (one hidden layer of 4 neurons (or units) and one output layer with 2 neurons), and three inputs. Right: A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer.
Take a two layer neural network as an example. You do following steps to train a neural network model:
-
Initialize the weights. Between input layer and hidden layer, there is matrix $ W1 $ for input weights. Between hidden layer and output layer, there is matrix $ W2 $ for hidden layer weights. We first initialize them.
-
Forwardpropagation(forward pass). We do forward pass to compute the loss. Say, for the first layer, we use ReLU as activation function and softmax for the second layer. So we have the following expressions. Then, we get the loss.
\[HiddenLayer_{in} = X \times W1 + b1\] \[HiddenLayer_{out} = max(0, HiddenLayer_{in})\] \[OutputLayer_{in} = HiddenLayer_{out} \times W2 + b2\] \[OutputLayer_{out} = softmax(OutputLayer_{in})\] -
Backpropagation. We calculate the gradient for decreasing the loss. According the expression above, we compute the corresponding gradients of every layer for every $ W $ and $ b $(bias). The math behind can be referred to this blog.
-
Train the network using SGD. It means that we use the computed gradients to tweak our parameters($ W $ and $ b $), making the loss converge into a minimal. The final trained parameters are the key part of our model. Check the code below to see how it is implemented.
Here is an implement of the loss and the gradients:
def loss(self, X, y=None, reg=0.0):
"""
Compute the loss and gradients for a two layer fully connected neural
network.
Inputs:
- X: Input data of shape (N, D). Each X[i] is a training sample.
- y: Vector of training labels. y[i] is the label for X[i], and each y[i] is
an integer in the range 0 <= y[i] < C. This parameter is optional; if it
is not passed then we only return scores, and if it is passed then we
instead return the loss and gradients.
- reg: Regularization strength.
Returns:
If y is None, return a matrix scores of shape (N, C) where scores[i, c] is
the score for class c on input X[i].
If y is not None, instead return a tuple of:
- loss: Loss (data loss and regularization loss) for this batch of training
samples.
- grads: Dictionary mapping parameter names to gradients of those parameters
with respect to the loss function; has the same keys as self.params.
"""
# Unpack variables from the params dictionary
W1, b1 = self.params['W1'], self.params['b1']
W2, b2 = self.params['W2'], self.params['b2']
N, D = X.shape
# Compute the forward pass
scores = None
#############################################################################
# TODO: Perform the forward pass, computing the class scores for the input. #
# Store the result in the scores variable, which should be an array of #
# shape (N, C). #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
hidden_layer = np.maximum(0, X.dot(W1) + b1)
scores = (hidden_layer).dot(W2) + b2
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# If the targets are not given then jump out, we're done
if y is None:
return scores
# Compute the loss
loss = None
#############################################################################
# TODO: Finish the forward pass, and compute the loss. This should include #
# both the data loss and L2 regularization for W1 and W2. Store the result #
# in the variable loss, which should be a scalar. Use the Softmax #
# classifier loss. #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
log_term = np.sum(np.exp(scores), axis=1)
loss = np.sum(- scores[np.arange(X.shape[0]), y] +
np.log(log_term))
loss /= X.shape[0]
loss += reg * np.sum(W1 * W1) + reg * np.sum(W2 * W2)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Backward pass: compute gradients
grads = {}
#############################################################################
# TODO: Compute the backward pass, computing the derivatives of the weights #
# and biases. Store the results in the grads dictionary. For example, #
# grads['W1'] should store the gradient on W1, and be a matrix of same size #
#############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
index = np.zeros_like(scores)
index[np.arange(N), y] = 1
ds = np.exp(scores) / log_term.reshape(N, 1)
ds = (ds - index) / N
dW2 = hidden_layer.T.dot(ds)
dW2 += 2 * reg * W2
db2 = np.sum(ds, axis=0,keepdims=False)
dhidden = np.dot(ds, W2.T)
dhidden[hidden_layer <= 0] = 0
dW1 = X.T.dot(dhidden)
dW1 += 2 * reg * W1
db1 = np.sum(dhidden, axis=0, keepdims=False)
grads['W2'] = dW2
grads['b2'] = db2
grads['W1'] = dW1
grads['b1'] = db1
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return loss, grads
def train(self, X, y, X_val, y_val,
learning_rate=1e-3, learning_rate_decay=0.95,
reg=5e-6, num_iters=100,
batch_size=200, verbose=False):
"""
Train this neural network using stochastic gradient descent.
Inputs:
- X: A numpy array of shape (N, D) giving training data.
- y: A numpy array f shape (N,) giving training labels; y[i] = c means that
X[i] has label c, where 0 <= c < C.
- X_val: A numpy array of shape (N_val, D) giving validation data.
- y_val: A numpy array of shape (N_val,) giving validation labels.
- learning_rate: Scalar giving learning rate for optimization.
- learning_rate_decay: Scalar giving factor used to decay the learning rate
after each epoch.
- reg: Scalar giving regularization strength.
- num_iters: Number of steps to take when optimizing.
- batch_size: Number of training examples to use per step.
- verbose: boolean; if true print progress during optimization.
"""
num_train = X.shape[0]
iterations_per_epoch = max(num_train / batch_size, 1)
# Use SGD to optimize the parameters in self.model
loss_history = []
train_acc_history = []
val_acc_history = []
for it in range(num_iters):
X_batch = None
y_batch = None
#########################################################################
# TODO: Create a random minibatch of training data and labels, storing #
# them in X_batch and y_batch respectively. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
mask = np.random.choice(np.arange(num_train), batch_size, replace=True)
X_batch = X[mask]
y_batch = y[mask]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Compute loss and gradients using the current minibatch
loss, grads = self.loss(X_batch, y=y_batch, reg=reg)
loss_history.append(loss)
#########################################################################
# TODO: Use the gradients in the grads dictionary to update the #
# parameters of the network (stored in the dictionary self.params) #
# using stochastic gradient descent. You'll need to use the gradients #
# stored in the grads dictionary defined above. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for param_name in grads:
self.params[param_name] += - learning_rate * grads[param_name]
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
if verbose and it % 100 == 0:
print('iteration %d / %d: loss %f' % (it, num_iters, loss))
# Every epoch, check train and val accuracy and decay learning rate.
if it % iterations_per_epoch == 0:
# Check accuracy
train_acc = (self.predict(X_batch) == y_batch).mean()
val_acc = (self.predict(X_val) == y_val).mean()
train_acc_history.append(train_acc)
val_acc_history.append(val_acc)
# Decay learning rate
learning_rate *= learning_rate_decay
return {
'loss_history': loss_history,
'train_acc_history': train_acc_history,
'val_acc_history': val_acc_history,
}
Debug the Training and Tuning the Hyperparameters
Another work we need to do is tuning the hyperparameters, which is also important and even hard. Here is a paragraph form CS231n:
Tuning. Tuning the hyperparameters and developing intuition for how they affect the final performance is a large part of using Neural Networks, so we want you to get a lot of practice. Below, you should experiment with different values of the various hyperparameters, including hidden layer size, learning rate, numer of training epochs, and regularization strength. You might also consider tuning the learning rate decay, but you should be able to get good performance using the default value.
which means we need to try different hidden layer size, learning rate, number of iteration, regularization strength and so on for finding the best validation accuracy. Here is the implementation:
best_net = None # store the best model into this
#################################################################################
# TODO: Tune hyperparameters using the validation set. Store your best trained #
# model in best_net. #
# #
# To help debug your network, it may help to use visualizations similar to the #
# ones we used above; these visualizations will have significant qualitative #
# differences from the ones we saw above for the poorly tuned network. #
# #
# Tweaking hyperparameters by hand can be fun, but you might find it useful to #
# write code to sweep through possible combinations of hyperparameters #
# automatically like we did on the previous exercises. #
#################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
input_size = 32 * 32 * 3
num_classes = 10
best_val = -1
learning_rates = [9e-2, 1e-3, 2e-3, 3e-3, 4e-3]
hidden_sizes = [50, 100, 150]
num_iterses = [1000, 1500, 2000, 2500]
regularization_strengths = [0.1, 0.25, 0.5]
for lr in range(len(learning_rates)):
for hz in range(len(hidden_sizes)):
for ni in range(len(num_iterses)):
for rs in range(len(regularization_strengths)):
net_th = TwoLayerNet(input_size, hidden_sizes[hz], num_classes)
# Train the network
stats = net_th.train(X_train, y_train, X_val, y_val,
num_iters=num_iterses[ni], batch_size=200,
learning_rate=learning_rates[lr], learning_rate_decay=0.95,
reg=regularization_strengths[rs], verbose=True)
y_train_pred = net_th.predict(X_train)
training_accuracy = (np.mean(y_train == y_train_pred))
#print('training accuracy: %f' % (np.mean(y_train == y_train_pred), ))
y_val_pred = net_th.predict(X_val)
validation_accuracy = (np.mean(y_val == y_val_pred))
#print('validation accuracy: %f' % (np.mean(y_val == y_val_pred), ))
if validation_accuracy > best_val:
best_val = validation_accuracy
best_net = net_th
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
Reference
Backpropagation, Intuitions Neural Networks Part 1: Setting up the Architecture
Assignment #1: Image Classification, kNN, SVM, Softmax, Neural Network